알고리즘

[알고리즘] 그래프-너비 우선 탐색, 깊이 우선 탐색, 최단경로 알고리즘(다익스트라 알고리즘), 최소 신장트리 알고리즘(크루스칼 알고리즘, 프림 알고리즘)

framecreator 2021. 11. 16. 15:36

*** 아래의 내용은 패스트 캠퍼스 알고리즘 강의 자료(이준희 강사님 저)를 강의를 들으면서 정리한 내용입니다. ***

1. 그래프 (Graph) 이해

(1) 그래프 기본 개념

그래프는 실제 세계의 현상이나 사물을 정점(Vertex) 또는 노드(Node) 와 간선(Edge)로 표현하기 위해 사용
예제 집에서 회사로 가는 경로를 그래프로 표현한 예

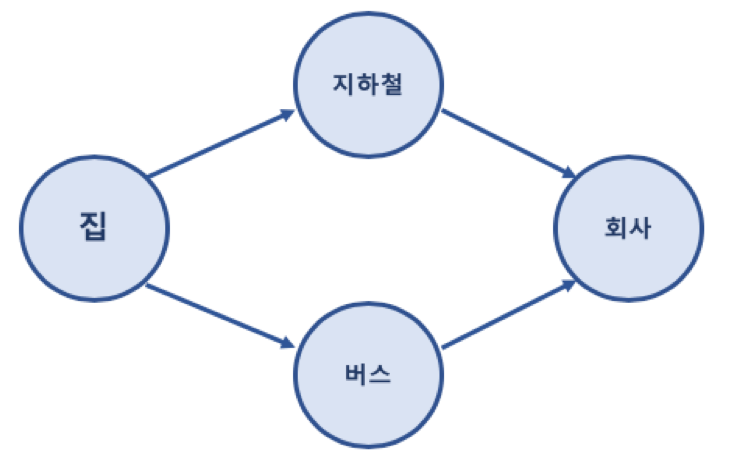
(2) 그래프 (Graph) 관련 용어

노드 (Node): 위치를 말함, 정점(Vertex)라고도 함
간선 (Edge): 위치 간의 관계를 표시한 선으로 노드를 연결한 선이라고 보면 됨 (link 또는 branch 라고도 함)
인접 정점 (Adjacent Vertex) : 간선으로 직접 연결된 정점(또는 노드)

참고 용어

정점의 차수 (Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
진입 차수 (In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
진출 차수 (Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
경로 길이 (Path Length): 경로를 구성하기 위해 사용된 간선의 수
단순 경로 (Simple Path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
사이클 (Cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우

단순 경로 (A-B-C)

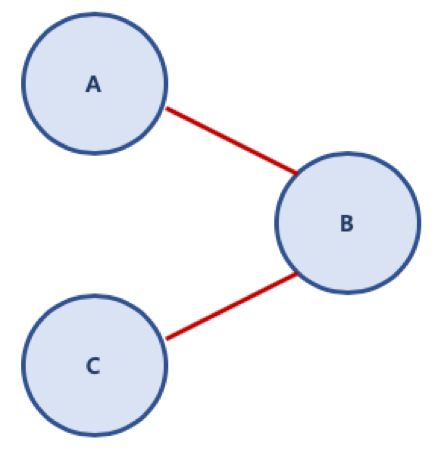
(3)그래프 (Graph) 종류

1)무방향 그래프 (Undirected Graph)

방향이 없는 그래프
간선을 통해, 노드는 양방향으로 갈 수 있음
보통 노드 A, B가 연결되어 있을 경우, (A, B) 또는 (B, A) 로 표기

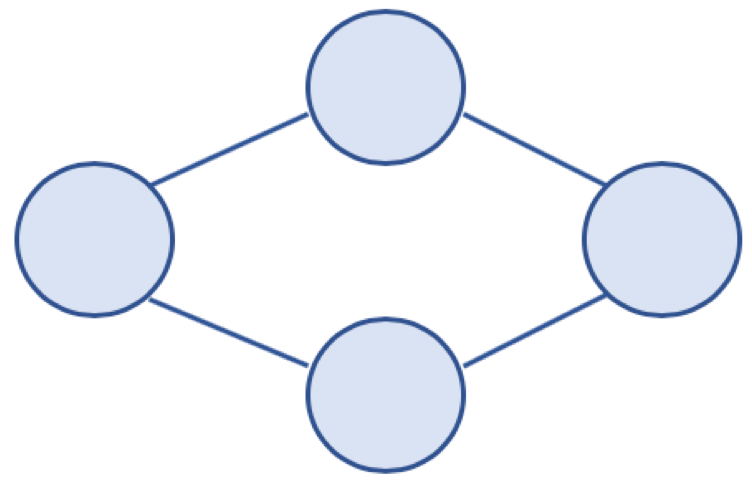
방향 그래프 (Directed Graph)

간선에 방향이 있는 그래프
보통 노드 A, B가 A -> B 로 가는 간선으로 연결되어 있을 경우, <A, B> 로 표기 (<B, A> 는 B -> A 로 가는 간선이 있는 경우이므로 <A, B> 와 다름)

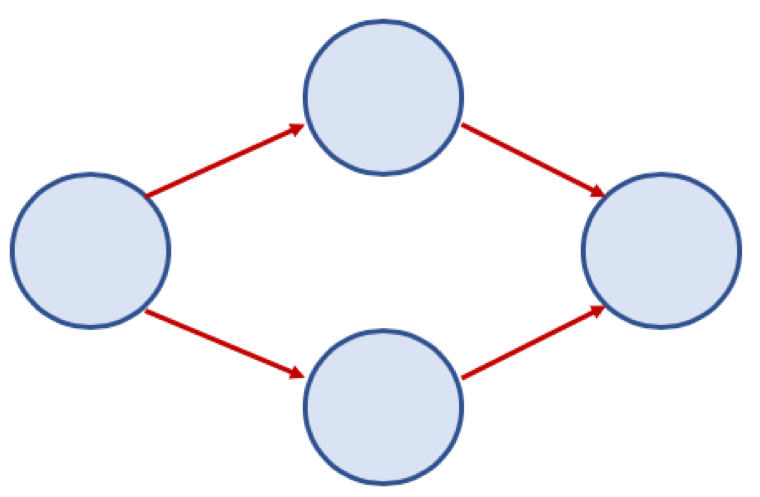
가중치 그래프 (Weighted Graph) 또는 네트워크 (Network)

간선에 비용 또는 가중치가 할당된 그래프

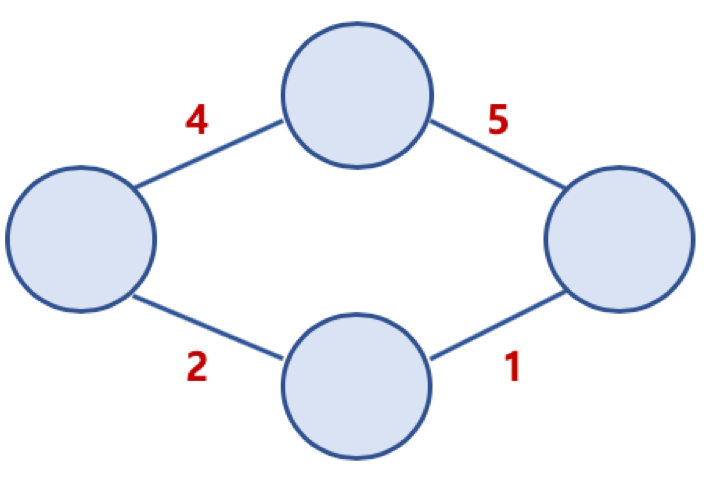
연결 그래프 (Connected Graph) 와 비연결 그래프 (Disconnected Graph)

연결 그래프 (Connected Graph)

무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우

비연결 그래프 (Disconnected Graph)

무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우

비연결 그래프

사이클 (Cycle) 과 비순환 그래프 (Acyclic Graph)

사이클 (Cycle)

단순 경로의 시작 노드와 종료 노드가 동일한 경우

비순환 그래프 (Acyclic Graph)

사이클이 없는 그래프

비순환 그래프

완전 그래프 (Complete Graph)

그래프의 모든 노드가 서로 연결되어 있는 그래프

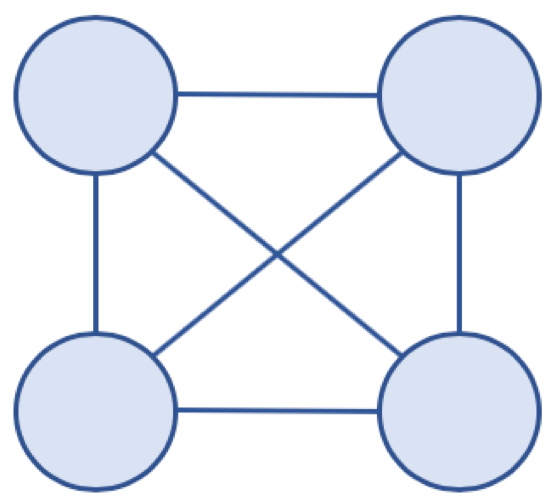
완전 그래프

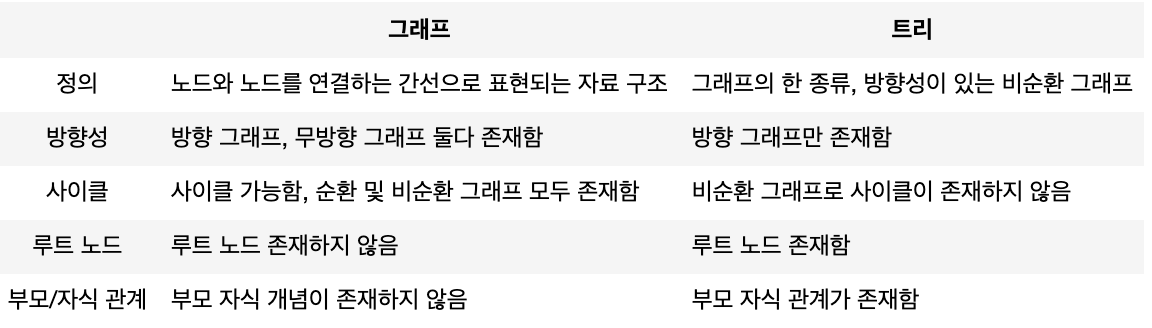
그래프와 트리의 차이

트리는 그래프 중에 속한 특별한 종류라고 볼 수 있음

2. BFS 와 DFS 란?

대표적인 그래프 탐색 알고리즘
너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식

BFS/DFS 방식 이해를 위한 예제

BFS 방식: A — B — C — D — G — H — I — E — F — J
한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
DFS 방식: A — B — D — E — F — C — G — H — I — J
한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함

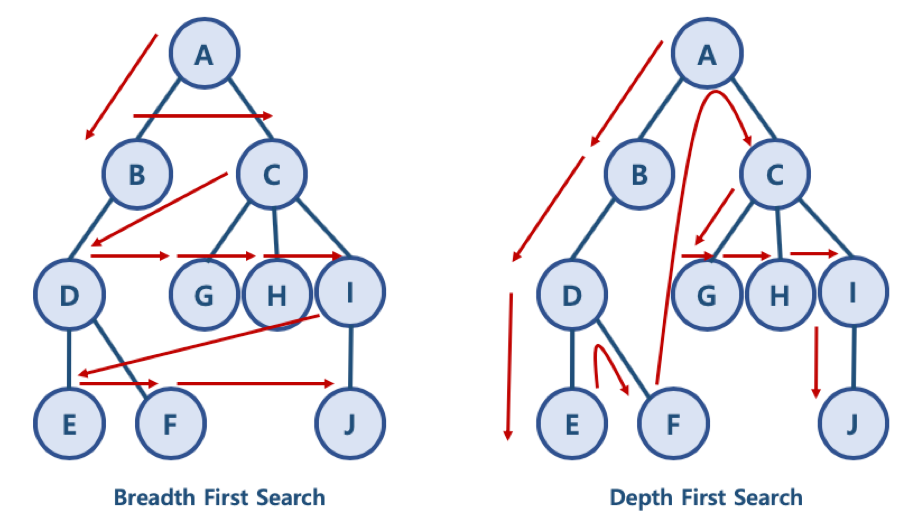
BFS와 DFS

그래프 표현 예

DFS 알고리즘 구현

자료구조 스택과 큐를 활용함
need_visit 스택과 visited 큐, 두 개의 자료 구조를 생성
BFS 자료구조는 두 개의 큐를 활용하는데 반해, DFS 는 스택과 큐를 활용한다는 차이가 있음을 인지해야 함

DFS 시간 복잡도

일반적인 DFS 시간 복잡도
노드 수: V
간선 수: E
시간 복잡도: O(V + E)

BFS 알고리즘 구현

자료구조 큐를 활용함
need_visit 큐와 visited 큐, 두 개의 큐를 생성

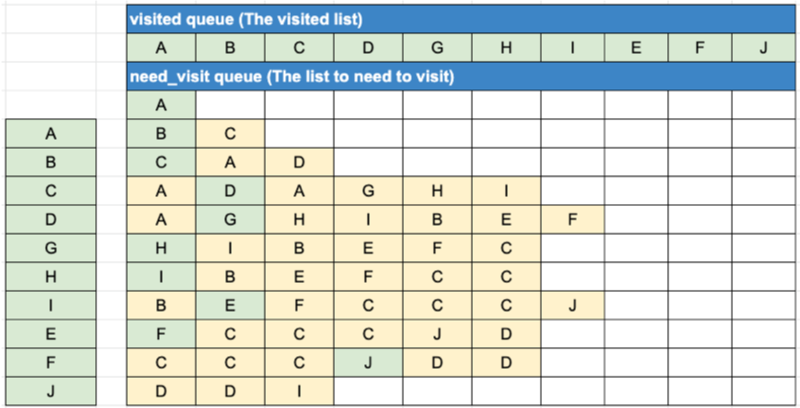
BFS 시간 복잡도

일반적인 BFS 시간 복잡도
노드 수: V
간선 수: E
시간 복잡도: O(V + E)

3. 최단 경로 알고리즘

1) 최단 경로 문제란?

최단 경로 문제란 두 노드를 잇는 가장 짧은 경로를 찾는 문제임
가중치 그래프 (Weighted Graph) 에서 간선 (Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적

최단 경로 문제 종류

단일 출발 및 단일 도착 (single-source and single-destination shortest path problem) 최단 경로 문제

그래프 내의 특정 노드 u 에서 출발, 또다른 특정 노드 v 에 도착하는 가장 짧은 경로를 찾는 문제

2. 단일 출발 (single-source shortest path problem) 최단 경로 문제

그래프 내의 특정 노드 u 와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
따지고 보면 굉장히 헷갈릴 수 있으므로 명확히 하자면, 예를 들어 A, B, C, D 라는 노드를 가진 그래프에서 특정 노드를 A 라고 한다면, A 외 모든 노드인 B, C, D 각 노드와 A 간에 (즉, A — B, A — C, A — D) 각각 가장 짧은 경로를 찾는 문제를 의미함

3. 전체 쌍(all-pair) 최단 경로: 그래프 내의 모든 노드 쌍 (u, v) 에 대한 최단 경로를 찾는 문제

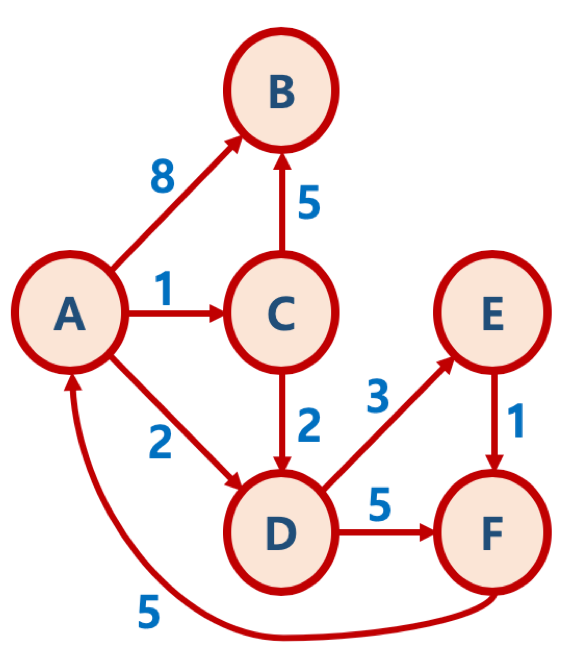
2) 최단 경로 알고리즘 — 다익스트라 알고리즘

다익스트라 알고리즘은 위의 최단 경로 문제 종류 중, 2번에 해당
하나의 정점에서 다른 모든 정점 간의 각각 가장 짧은 거리를 구하는 문제

다익스트라 알고리즘 로직

첫 정점을 기준으로 연결되어 있는 정점들을 추가해 가며, 최단 거리를 갱신하는 기법
다익스트라 알고리즘은 너비우선탐색(BFS)와 유사
첫 정점부터 각 노드간의 거리를 저장하는 배열을 만든 후, 첫 정점의 인접 노드 간의 거리부터 먼저 계산하면서, 첫 정점부터 해당 노드간의 가장 짧은 거리를 해당 배열에 업데이트
다익스트라 알고리즘의 다양한 변형 로직이 있지만, 가장 개선된 우선순위 큐를 사용하는 방식에 집중해서 설명하기로 함

우선순위 큐를 활용한 다익스트라 알고리즘

우선순위 큐는 MinHeap 방식을 활용해서, 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼내게 됨
1) 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장함 (inf 라고 표현함)
우선순위 큐에 (첫 정점, 거리 0) 만 먼저 넣음
2) 우선순위 큐에서 노드를 꺼냄
처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
결과적으로 너비 우선 탐색 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 됨
만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음

3) 2번의 과정을 우선순위 큐에 꺼낼 노드가 없을 때까지 반복한다.

예제로 이해하는 다익스트라 알고리즘 (우선순위 큐 활용)

1단계: 초기화

첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
초기에는 첫 정점의 거리는 0, 나머지는 무한대로 저장함 (inf 라고 표현함)
우선순위 큐에 (첫 정점, 거리 0) 만 먼저 넣음

2단계: 우선순위 큐에서 추출한 (A, 0) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산

우선순위 큐에서 노드를 꺼냄
처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐
첫 정점에 인접한 노드들 각각에 대해, 첫 정점에서 각 노드로 가는 거리와 현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
배열에 저장되어 있는 거리보다, 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우, 배열에 해당 노드의 거리를 업데이트한다.
배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
결과적으로 너비 우선 탐색 방식과 유사하게, 첫 정점에 인접한 노드들을 순차적으로 방문하게 됨
만약 배열에 기록된 현재까지 발견된 가장 짧은 거리보다, 더 긴 거리(루트)를 가진 (노드, 거리)의 경우에는 해당 노드와 인접한 노드간의 거리 계산을 하지 않음
이전 표에서 보듯이, 첫 정점 이외에 모두 inf 였었으므로, 첫 정점에 인접한 노드들은 모두 우선순위 큐에 들어가고, 첫 정점과 인접한 노드간의 거리가 배열에 업데이트됨

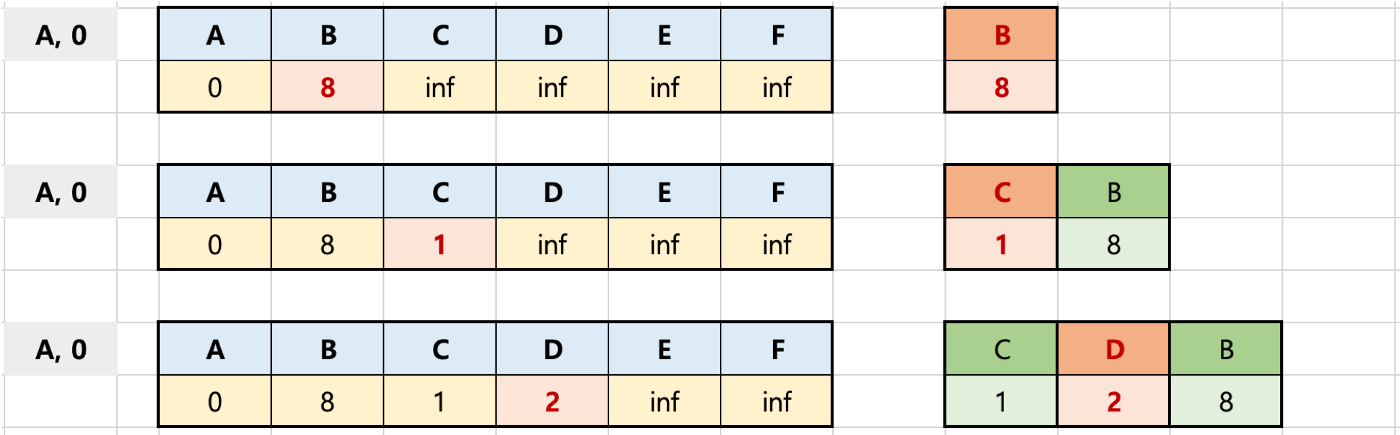
3단계: 우선순위 큐에서 (C, 1) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산

우선순위 큐가 MinHeap(최소 힙) 방식이므로, 위 표에서 넣어진 (C, 1), (D, 2), (B, 8) 중 (C, 1) 이 먼저 추출됨 (pop)
위 표에서 보듯이 1단계까지의 A — B 최단 거리는 8 인 상황임
A — C 까지의 거리는 1, C 에 인접한 B, D에서 C — B는 5, 즉 A — C — B 는 1 + 5 = 6 이므로, A — B 최단 거리 8보다 더 작은 거리를 발견, 이를 배열에 업데이트
배열에 업데이트했으므로 B, 6 (즉 A에서 B까지의 현재까지 발견한 최단 거리) 값이 우선순위 큐에 넣어짐
C — D 의 거리는 2, 즉 A — C — D 는 1 + 2 = 3 이므로, A — D의 현재 최단 거리인 2 보다 긴 거리, 그래서 D 의 거리는 업데이트되지 않음

4단계: 우선순위 큐에서 (D, 2) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산

지금까지 접근하지 못했던 E와 F 거리가 계산됨
A — D 까지의 거리인 2 에 D — E 가 3 이므로 이를 더해서 E, 5
A — D 까지의 거리인 2 에 D — F 가 5 이므로 이를 더해서 F, 7

5단계: 우선순위 큐에서 (E, 5) [노드, 첫 노드와의 거리] 를 기반으로 인접한 노드와의 거리 계산

A — E 거리가 5인 상태에서, E에 인접한 F를 가는 거리는 1, 즉 A — E — F 는 5 + 1 = 6, 현재 배열에 A — F 최단거리가 7로 기록되어 있으므로, F, 6 으로 업데이트
우선순위 큐에 F, 6 추가

6단계: 우선순위 큐에서 (B, 6), (F, 6) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산

예제의 방향 그래프에서 B 노드는 다른 노드로 가는 루트가 없음
F 노드는 A 노드로 가는 루트가 있으나, 현재 A — A 가 0 인 반면에 A — F — A 는 6 + 5 = 11, 즉 더 긴 거리이므로 업데이트되지 않음

7단계: 우선순위 큐에서 (F, 7), (B, 8) 를 순차적으로 추출해 각 노드 기반으로 인접한 노드와의 거리 계산

A — F 로 가는 하나의 루트의 거리가 7 인 상황이나, 배열에서 이미 A — F 로 가는 현재의 최단 거리가 6인 루트의 값이 있는 상황이므로, 더 긴거리인 F, 7 루트 기반 인접 노드까지의 거리는 계산할 필요가 없음, 그래서 계산없이 스킵함
계산하더라도 A — F 거리가 6인 루트보다 무조건 더 긴거리가 나올 수 밖에 없음
B, 8 도 현재 A — B 거리가 6이므로, 인접 노드 거리 계산이 필요 없음.

우선순위 큐를 사용하면 불필요한 계산 과정을 줄일 수 있음

우선순위 큐 사용 장점

지금까지 발견된 가장 짧은 거리의 노드에 대해서 먼저 계산
더 긴 거리로 계산된 루트에 대해서는 계산을 스킵할 수 있음

시간 복잡도

위 다익스트라 알고리즘은 크게 다음 두 가지 과정을 거침

과정1: 각 노드마다 인접한 간선들을 모두 검사하는 과정
과정2: 우선순위 큐에 노드/거리 정보를 넣고 삭제(pop)하는 과정

각 과정별 시간 복잡도

과정1: 각 노드는 최대 한 번씩 방문하므로 (첫 노드와 해당 노드간의 갈 수 있는 루트가 있는 경우만 해당), 그래프의 모든 간선은 최대 한 번씩 검사
즉, 각 노드마다 인접한 간선들을 모두 검사하는 과정은 O(E) 시간이 걸림, E 는 간선(edge)의 약자
과정2: 우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 경우, 우선순위 큐에 노드/거리 정보를 넣고, 삭제하는 과정이 최악의 시간이 걸림
우선순위 큐에 가장 많은 노드, 거리 정보가 들어가는 시나리오는 그래프의 모든 간선이 검사될 때마다, 배열의 최단 거리가 갱신되고, 우선순위 큐에 노드/거리가 추가되는 것임
이 때 추가는 각 간선마다 최대 한 번 일어날 수 있으므로, 최대 O(E)의 시간이 걸리고, O(E) 개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 𝑂(𝑙𝑜𝑔𝐸)가 걸림
따라서 해당 과정의 시간 복잡도는 𝑂(𝐸𝑙𝑜𝑔𝐸)

총 시간 복잡도

과정1 + 과정2 = O(E) + 𝑂(𝐸𝑙𝑜𝑔𝐸) = 𝑂(𝐸+𝐸𝑙𝑜𝑔𝐸)=𝑂(𝐸𝑙𝑜𝑔𝐸))

참고: 힙의 시간 복잡도

depth (트리의 높이) 를 h라고 표기한다면,
n개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 h=log2n 에 가까우므로, 시간 복잡도는 O(logn)

4. 최소 신장 트리

(1) 신장 트리 란?

Spanning Tree, 또는 신장 트리 라고 불리움 (Spanning Tree가 보다 자연스러워 보임)
원래의 그래프의 모든 노드가 연결되어 있으면서 트리의 속성을 만족하는 그래프

신장 트리의 조건

본래의 그래프의 모든 노드를 포함해야 함
모든 노드가 서로 연결
트리의 속성을 만족시킴 (사이클이 존재하지 않음)

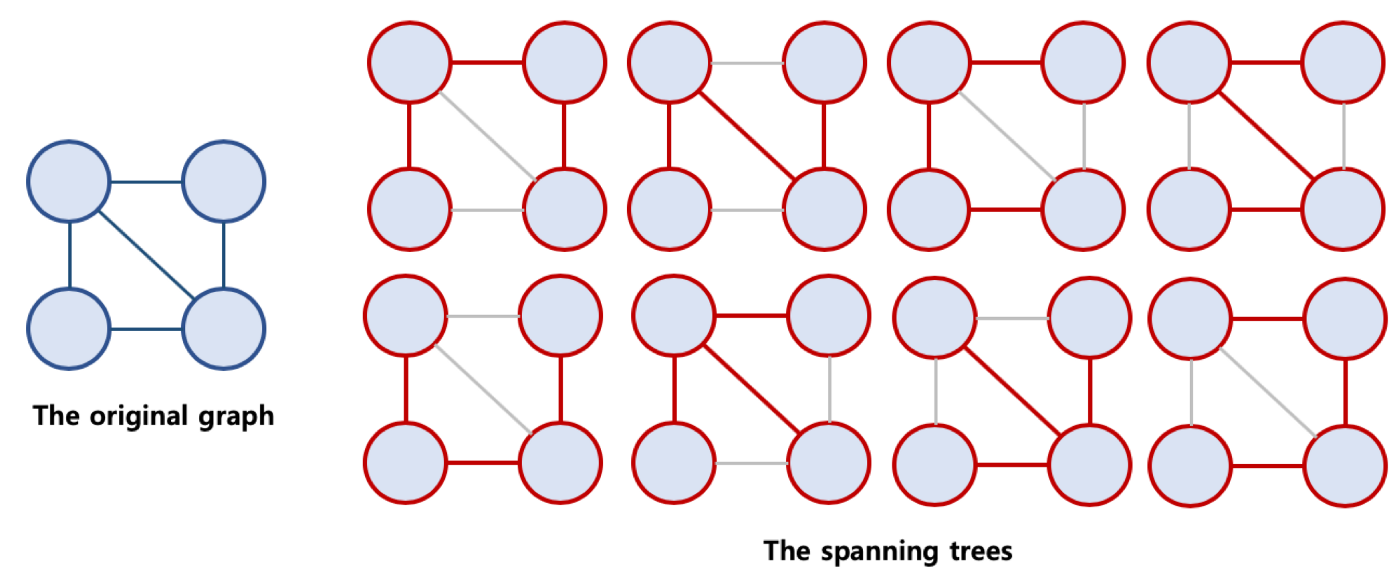
(2) 최소 신장 트리

Minimum Spanning Tree, MST 라고 불리움
가능한 Spanning Tree 중에서, 간선의 가중치 합이 최소인 Spanning Tree를 지칭함

(3) 최소 신장 트리 알고리즘

그래프에서 최소 신장 트리를 찾을 수 있는 알고리즘이 존재함
대표적인 최소 신장 트리 알고리즘
Kruskal’s algorithm (크루스칼 알고리즘), Prim’s algorithm (프림 알고리즘)

(4) 크루스칼 알고리즘 (Kruskal’s algorithm)

모든 정점을 독립적인 집합으로 만든다.
모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.
두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)
탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)

크루스컬 알고리즘의 시간 복잡도는 O(E log E)

다음 단계에서 2번, 간선을 비용 기준으로 정렬하는 시간에 좌우됨 (즉 간선을 비용 기준으로 정렬하는 시간이 가장 큼)

모든 정점을 독립적인 집합으로 만든다.
모든 간선을 비용을 기준으로 정렬하고, 비용이 작은 간선부터 양 끝의 두 정점을 비교한다.

퀵소트를 사용한다면 시간 복잡도는 O(n log n) 이며, 간선이 n 이므로 O(E log E)

3. 두 정점의 최상위 정점을 확인하고, 서로 다를 경우 두 정점을 연결한다. (최소 신장 트리는 사이클이 없으므로, 사이클이 생기지 않도록 하는 것임)

union-by-rank 와 path compression 기법 사용시 시간 복잡도가 결국 상수값에 가까움. O(1)

(5) Union-Find 알고리즘

Disjoint Set을 표현할 때 사용하는 알고리즘으로 트리 구조를 활용하는 알고리즘
간단하게, 노드들 중에 연결된 노드를 찾거나, 노드들을 서로 연결할 때 (합칠 때) 사용

Disjoint Set이란

서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
공통 원소가 없는 (서로소) 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조를 의미함
Disjoint Set = 서로소 집합 자료구조

초기화

n 개의 원소가 개별 집합으로 이뤄지도록 초기화

2. Union

두 개별 집합을 하나의 집합으로 합침, 두 트리를 하나의 트리로 만듬

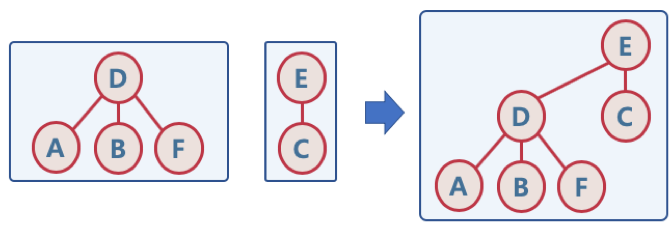
3. Find

여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인

Union-Find 알고리즘의 고려할 점

Union 순서에 따라서, 최악의 경우 링크드 리스트와 같은 형태가 될 수 있음.
이 때는 Find/Union 시 계산량이 O(N) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용함

1) union-by-rank 기법

각 트리에 대해 높이(rank)를 기억해 두고,
Union시 두 트리의 높이(rank)가 다르면, 높이가 작은 트리를 높이가 큰 트리에 붙임 (즉, 높이가 큰 트리의 루트 노드가 합친 집합의 루트 노드가 되게 함)

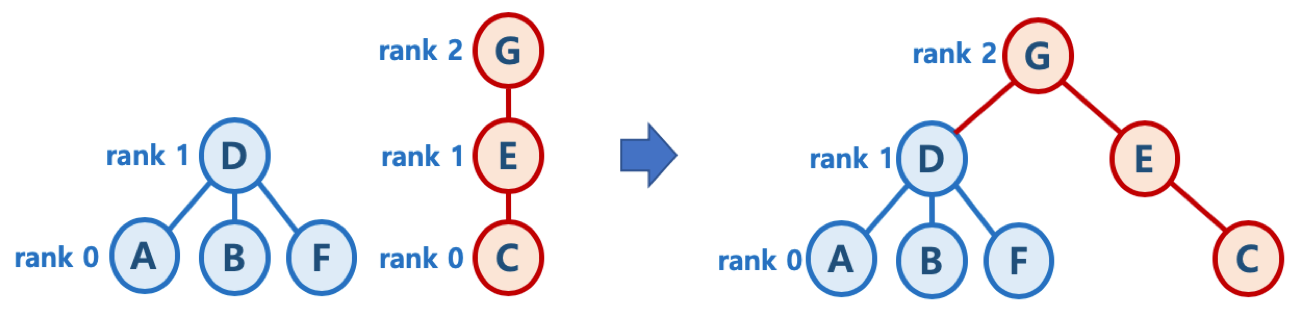
높이가 h — 1 인 두 개의 트리를 합칠 때는 한 쪽의 트리 높이를 1 증가시켜주고, 다른 쪽의 트리를 해당 트리에 붙여줌

초기화시, 모든 원소는 높이(rank) 가 0 인 개별 집합인 상태에서, 하나씩 원소를 합칠 때, union-by-rank 기법을 사용한다면,
높이가 h 인 트리가 만들어지려면, 높이가 h-1 인 두 개의 트리가 합쳐져야 함
높이가 h -1 인 트리를 만들기 위해 최소 n개의 원소가 있어야 한다면, 높이가 h 인 트리가 만들어지기 위해서는 최소 2n개의 원소가 있어야 함
따라서 union-by-rank 기법을 사용하면, union/find 연산의 시간복잡도는 O(N) 이 아닌, O(logN) 로 낮출 수 있음

2) path compression

Find를 실행한 노드에서 거쳐간 노드를 루트에 다이렉트로 연결하는 기법
Find를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있음

union-by-rank 와 path compression 기법 사용시 시간 복잡도는 다음 계산식을 만족함이 증명되었음
O(Mlog∗N)
log∗N 은 다음 값을 가짐이 증명되었음
N이 2의65536 제곱값을 가지더라도,log∗N 의 값이 5의 값을 가지므로, 거의 O(1), 즉 상수값에 가깝다고 볼 수 있음.

패스트캠퍼스 알고리즘 강의 자료

(6)프림 알고리즘

1) 프림 알고리즘 (Prim’s algorithm)이란?

대표적인 최소 신장 트리 알고리즘

Kruskal’s algorithm (크루스칼 알고리즘), Prim’s algorithm (프림 알고리즘)

프림 알고리즘

시작 정점을 선택한 후, 정점에 인접한 간선중 최소 간선으로 연결된 정점을 선택하고, 해당 정점에서 다시 최소 간선으로 연결된 정점을 선택하는 방식으로 최소 신장 트리를 확장해가는 방식

Kruskal’s algorithm 과 Prim’s algorithm 비교

둘다, 탐욕 알고리즘을 기초로 하고 있음 (당장 눈 앞의 최소 비용을 선택해서, 결과적으로 최적의 솔루션을 찾음)
Kruskal’s algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구함
Prim’s algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함

2)그림으로 이해하는 프림 알고리즘

임의의 정점을 선택, ‘연결된 노드 집합’에 삽입
선택된 정점에 연결된 간선들을 간선 리스트에 삽입
간선 리스트에서 최소 가중치를 가지는 간선부터 추출해서,

해당 간선에 연결된 인접 정점이 ‘연결된 노드 집합’에 이미 들어 있다면, 스킵함(cycle 발생을 막기 위함)
해당 간선에 연결된 인접 정점이 ‘연결된 노드 집합’에 들어 있지 않으면, 해당 간선을 선택하고, 해당 간선 정보를 ‘최소 신장 트리’에 삽입

4. 추출한 간선은 간선 리스트에서 제거

5. 간선 리스트에 더 이상의 간선이 없을 때까지 3–4번을 반복

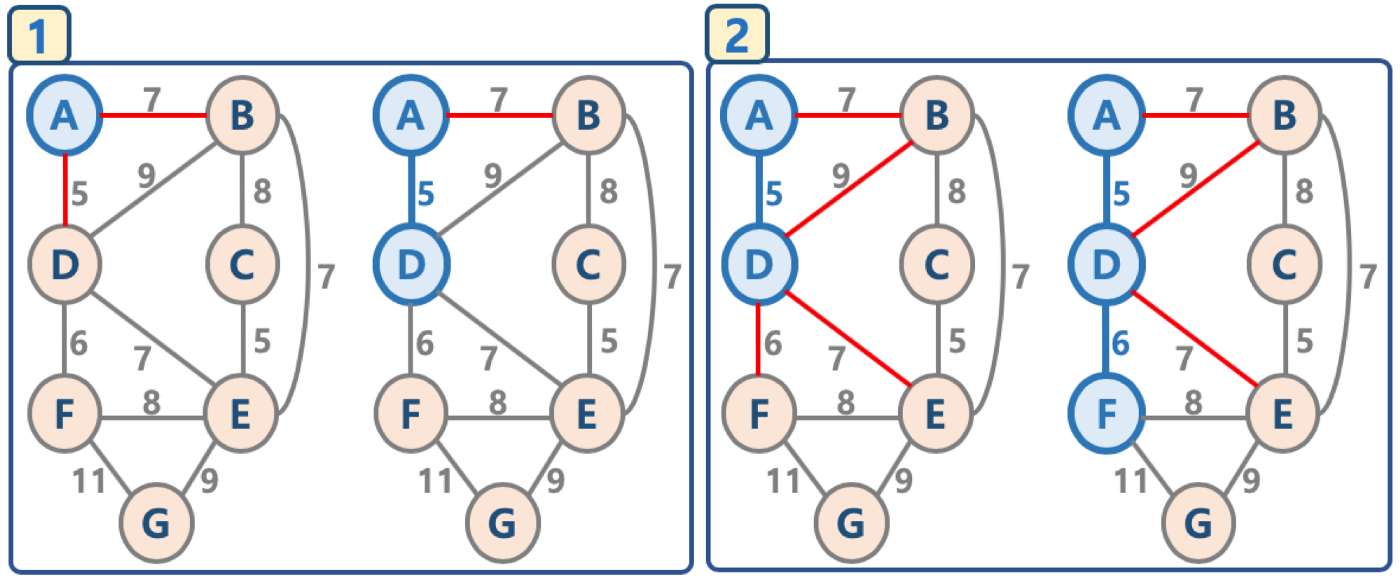
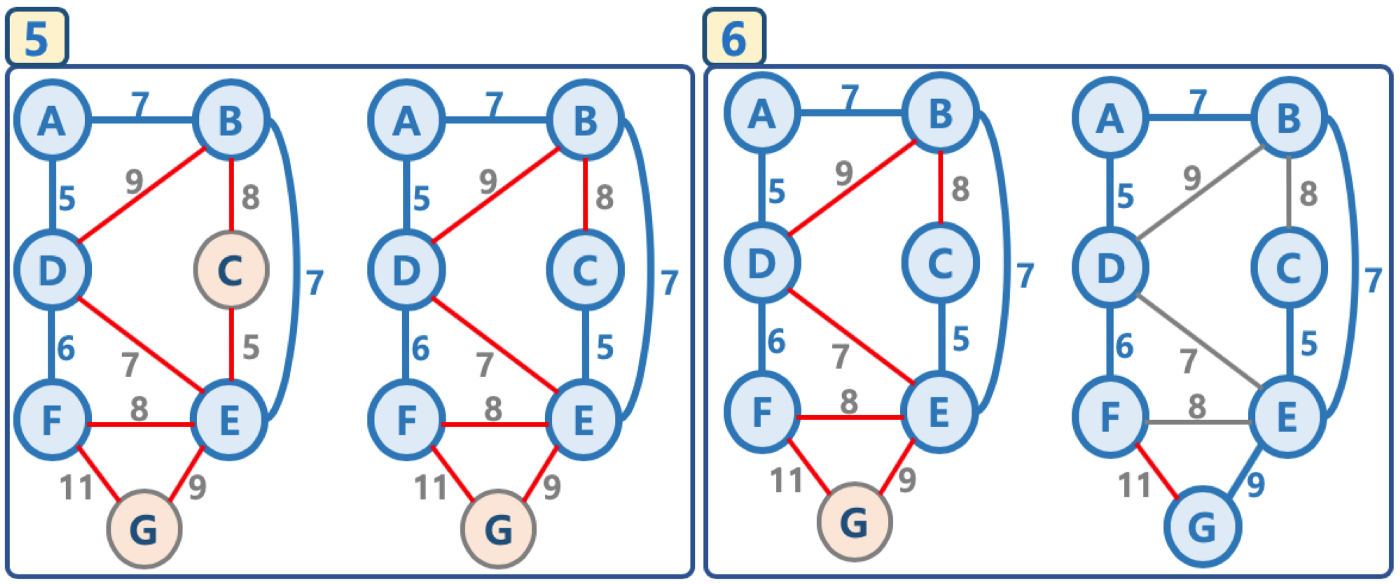
프림 알고리즘 시간 복잡도

최악의 경우, while 구문에서 모든 간선에 대해 반복하고, 최소 힙 구조를사용하므로 O(ElogE) 시간 복잡도를 가짐

참고: 개선된 프림 알고리즘

간선이 아닌 노드를 중심으로 우선순위 큐를 적용하는 방식
초기화 — 정점:key 구조를 만들어놓고, 특정 정점의 key값은 0, 이외의 정점들의 key값은 무한대로 놓음. 모든 정점:key 값은 우선순위 큐에 넣음
가장 key값이 적은 정점:key를 추출한 후(pop 하므로 해당 정점:key 정보는 우선순위 큐에서 삭제됨), (extract min 로직이라고 부름)
해당 정점의 인접한 정점들에 대해 key 값과 연결된 가중치 값을 비교하여 key값이 작으면 해당 정점:key 값을 갱신
정점:key 값 갱신시, 우선순위 큐는 최소 key값을 가지는 정점:key 를 루트노드로 올려놓도록 재구성함 (decrease key 로직이라고 부름)
개선된 프림 알고리즘 구현시 고려 사항

첫째, 우선순위 큐(최소힙) 구조에서, 이미 들어가 있는 데이터의 값 변경시, 최소값을 가지는 데이터를 루트 노드로 올려놓도록 재구성하는 기능이 필요함

둘째, 구현 복잡도를 줄이기 위해, heapdict 라이브러리를 통해, 해당 기능을 간단히 구현

(참고) 개선된 프림 알고리즘의 시간 복잡도: O(ElogV)

최초 key 생성 시간 복잡도: O(V)
while 구문과 keys.popitem() 의 시간 복잡도는 O(VlogV)
while 구문은 V(노드 갯수) 번 실행됨
heap 에서 최소 key 값을 가지는 노드 정보 추출 시(pop)의 시간 복잡도: O(logV)
for 구문의 총 시간 복잡도는 O(ElogV)
for 구문은 while 구문 반복시에 결과적으로 총 최대 간선의 수 E만큼 실행 가능O(E)
for 구문 안에서 key값 변경시마다 heap 구조를 변경해야 하며, heap 에는 최대 V 개의 정보가 있으므로 O(logV)
일반적인 heap 자료 구조 자체에는 본래 heap 내부의 데이터 우선순위 변경시, 최소 우선순위 데이터를 루트노드로 만들어주는 로직은 없음. 이를 decrease key 로직이라고 부름, 해당 로직은 heapdict 라이브러리를 활용해서 간단히 적용가능
따라서 총 시간 복잡도는 O(V+VlogV+ElogV) 이며,
O(V)는 전체 시간 복잡도에 큰 영향을 미치지 않으므로 삭제,
E > V 이므로 (최대 V2=E 가 될 수 있음), O((V+E)logV) 는 간단하게 O(ElogV) 로 나타낼 수 있음

위의 내용은 패스트 캠퍼스 알고리즘 강의 자료(이준희 강사님 저)를 강의를 들으면서 정리한 내용입니다. ***